
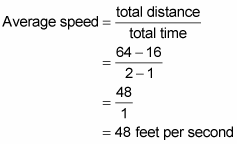
So, in order to calculate the average velocity of an object. Find the average velocity of the object over the following. The average velocity of an object is the change in its position over a period of time. As may be evident, in such an event, we will be finding instantaneous velocity instead of average velocity.Now as we squeeze this window between \(t=1\) and \(t=1+h\) down towards zero, the average velocity becomes the “instantaneous velocity” - just as the slope of the secant line becomes the slope of the tangent line. The position of an object moving along a line is given by the function s(t) 19(t)2 + 76 (t). Note that this leads to dividing by zero in cases where #a=b#. In other words, our general average velocity formula on an interval from #t=a# to #t=b# is Instead, our average velocity will be represented by the difference between our #x# values at the endpoints, divided by the elapsed units of #t#.
#AVERAGE VELOCITY FORMULA CALCULUS HOW TO#
If asked to find Timothy's average velocity over the course of #b# units of time (starting at #t=0#), the calculation is easier in that we do not need derivatives. Find average velocity over given intervalsFind average velocity over given intervalsToday were going to be talking about how to find average velocity over g. The velocity at t 10 is 10 m/s and the velocity at t 11 is 15 m/s. For our example, the bike's initial velocity v i is 5 m/s. If and only if the acceleration is constant, the average velocity is the same as the average of the final velocity and the initial velocity: (vf + vi)/2. Use this formula to find average velocity. return one of the following three items: the equation of the tangent line, the slope of the tangent line. For example, let’s calculate a using the example for constant a above. At t 5, the bike is moving right at 5+ (2) (5) 15 m/s. Average velocity as the slope of a secant line. Thus, for our given point, #x'(t_0) = 2(t_0)-5# Acceleration is measured as the change in velocity over change in time (V/t), where is shorthand for change in. (Recall that the derivative, or rate of change, of position (or displacement) with respect to time is simply velocity). The power rule informs us that #x'(t) = 2t -5#. Thus, at a given point #(t_0, x_0)#, we differentiate our function with respect to #t#.
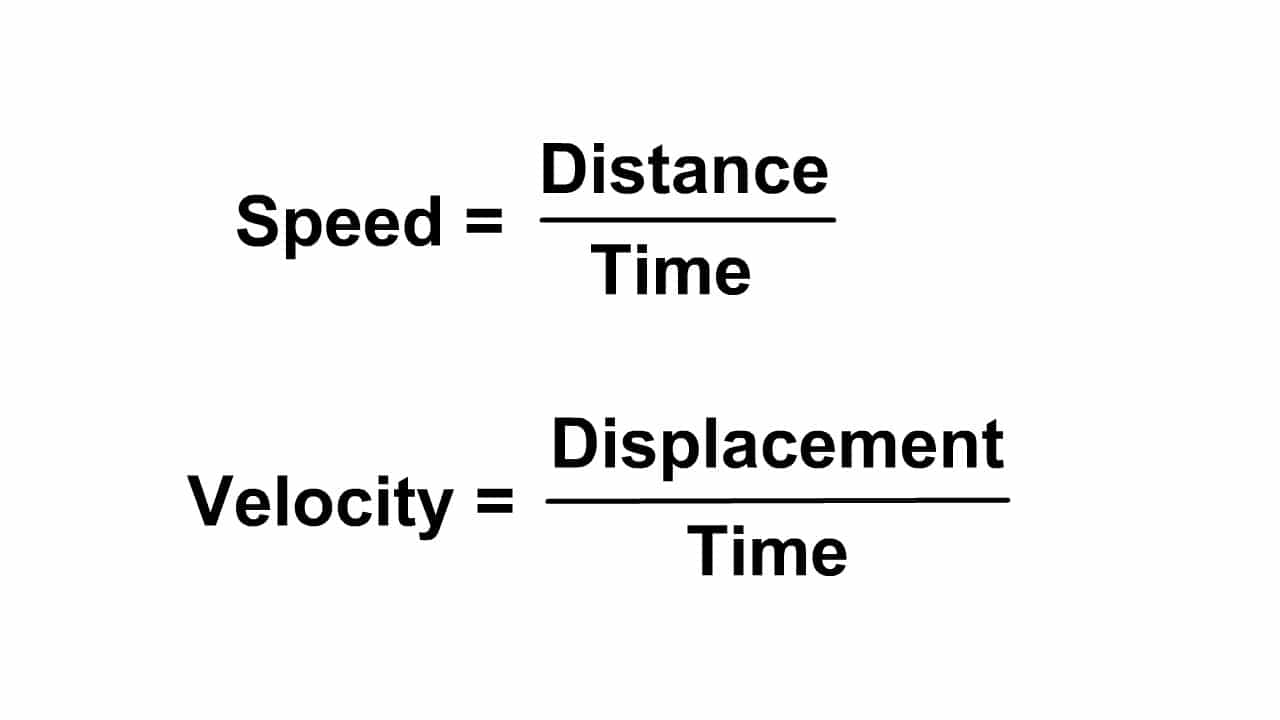
If asked to find Timothy's velocity at a given point, instantaneous velocity would fit best. In interests of simplicity, specific units shall be omitted. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us Creators.

Assume that Timothy's displacement function #x(t)# can be modeled as #x(t) = t^2 - 5t + 4#. For example, suppose Timothy is moving along a track of some kind. Typically, when confronted with a problem, it will be fairly evident whether instantaneous velocity or average velocity is called for. Meanwhile, the average velocity is equal to the slope of the secant line which intersects the function at the beginning and end of the interval. Graphically, the instantaneous velocity at any given point on a function #x(t)# is equal to the slope of the tangent line to the function at that location. The instantaneous velocity is the specific rate of change of position (or displacement) with respect to time at a single point #(x,t)#, while average velocity is the average rate of change of position (or displacement) with respect to time over an interval. You can find average acceleration by calculating the change in velocity (v) over the change in time (t) ( a v/t ).


 0 kommentar(er)
0 kommentar(er)
